Cross-validation: what is it and how should I use it?

Introduction

Cross-validation is a resampling method. The meaning of resampling is that we systematically draw samples from a training set and fit a specific model on each and every sample. We do this to see if there are differences in the results among the samples and we receive more knowledge than if we were to fit the model only on a single sample (the entire training set).

Let’s say we have a training set and a test set. At the end, we want to minimize the generalization error, that is, the expected prediction error over an independent test sample. This error can be expressed as follows:

,

which is the expected result of the loss function for a target result and the prediction model, given the training dataset. Common loss functions are the mean squared error (MSE), the mean absolute error (MAE), the mean bias error (MBE), the hinge loss, among many others.

We want to select a model that would return the lowest possible generalization error. To do that, we might want to test different model possibilities and assess their performance. Best practice tells you that when the training set is not large enough for you to properly estimate the generalization error from it, one of many possible techniques is cross-validation. There are different ways of doing cross-validation and I will briefly go over them in a bit. Before that, I just would like to mention another possible approach which is, for example, through a validation set: we estimate the test error by extracting a subset of the training set before fitting, which we call validation set, and then use statistical methods on it. This method, however, may lead to variable generalization error results and ends up using less data to fit the model, since we take part of the training set to form the validation set. As a consequence of using less data, we might end up with an overestimated test error. Cross-validation comes to work around these problems.

I recall that with cross-validation the idea is to assess a model and, after we are satisfied, apply it on the test set. I emphasize here that cross-validation is done on the training set and never on the test set. In Figure 1, we can see an example of a workflow for enhancing a model until we are happy with its parameters. Only then we can move on and perform the employ the model on the test set.

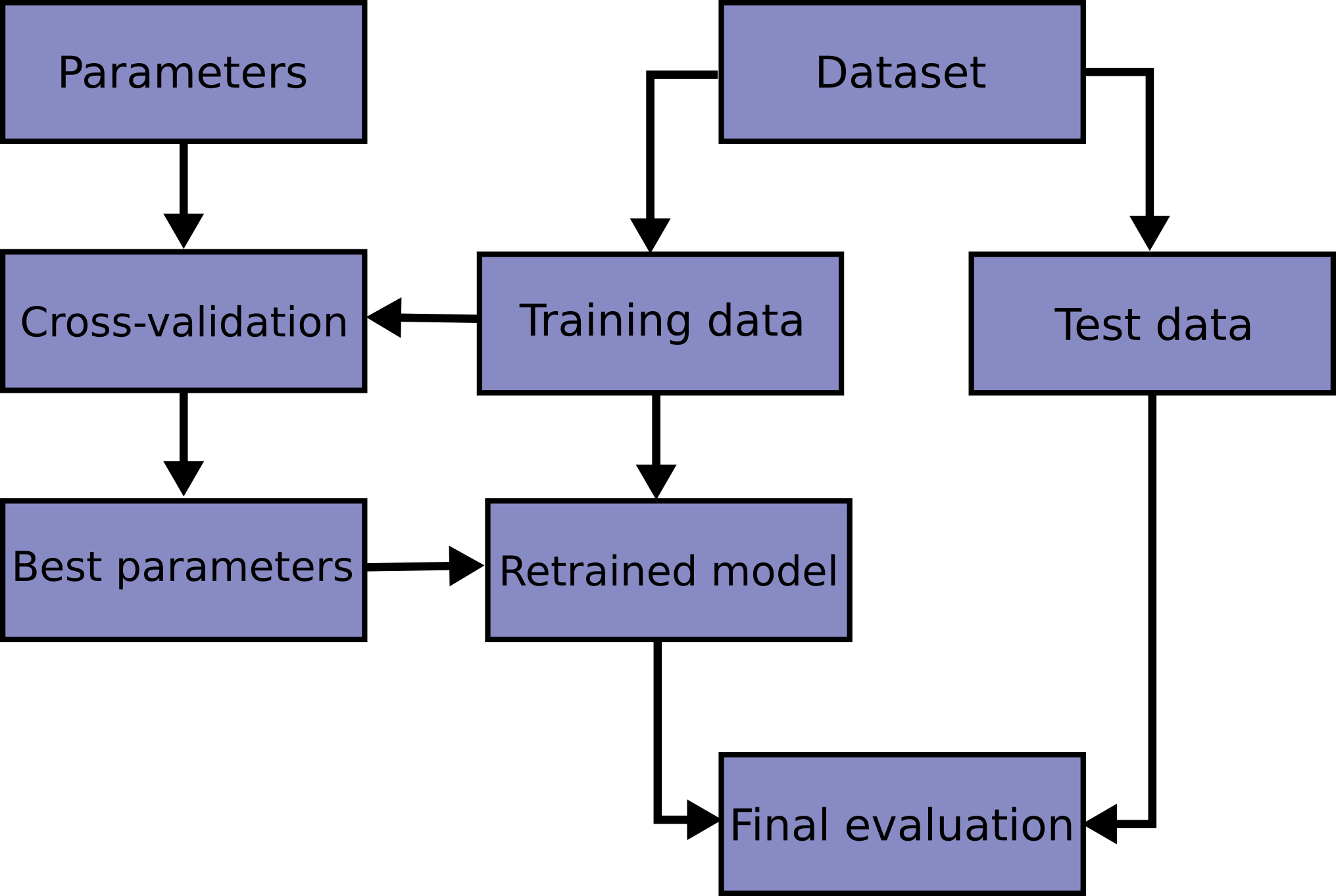Figure 1: A grid search workflow. Source: Scikit-learn.

In this article, I will go over:

1. K-Fold
2. Leave One Out (LOO)
3. Stratified K-Fold
4. Time Series Split

There are other types of cross-validation. For further information, please check the references at the bottom.

Cross-validation types

1. K-Fold

Description: K-Fold splits the training set into k groups, called folds. These folds are divided trying to achieve equally size groups, but they do not have to be exact. We fit our model using k-1 folds and the fold left out is used as a validation set. We compute the MSE on the validation fold and, at the end, we compute the average of all k MSEs.

MSE is defined as:

Where n is the number of observations, Y   is the true target value and Ŷ   is the predicted value. The K-Fold cross-validation, thus, is calculated as:

.

Common number of folds are 5 or 10. These numbers are usually used because they give more computational advantage than if we were to use n (the size of the training set). Look Figure 2 for an example using 3-Fold.

When to use it: When a random sample of the data does not represent well the underlying distribution.

When not to use it: Data points are not independent and identically distributed (i.i.d.).

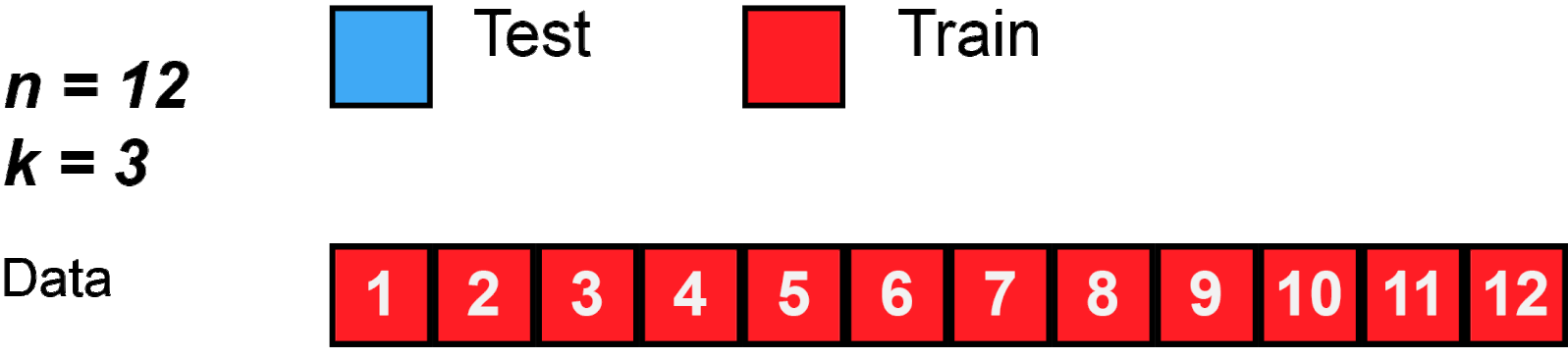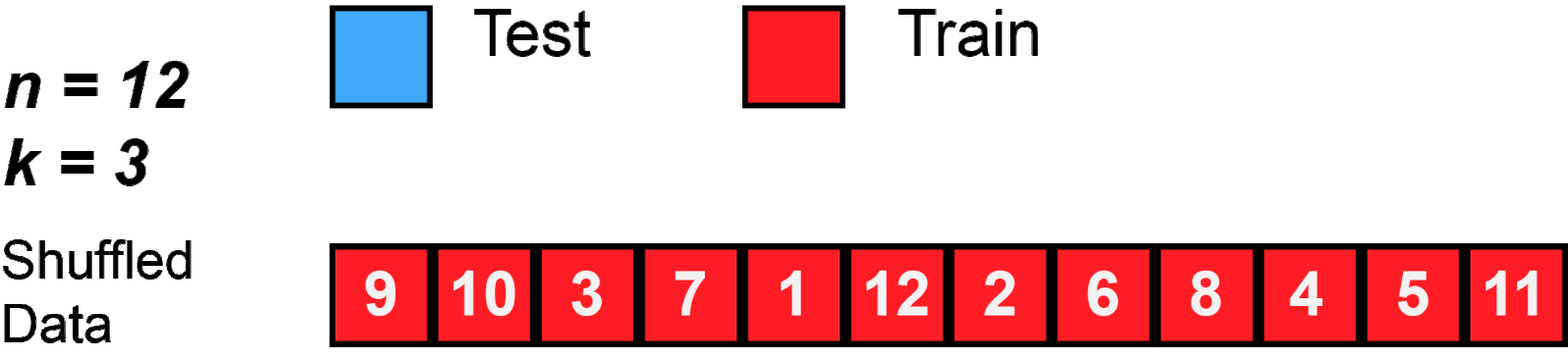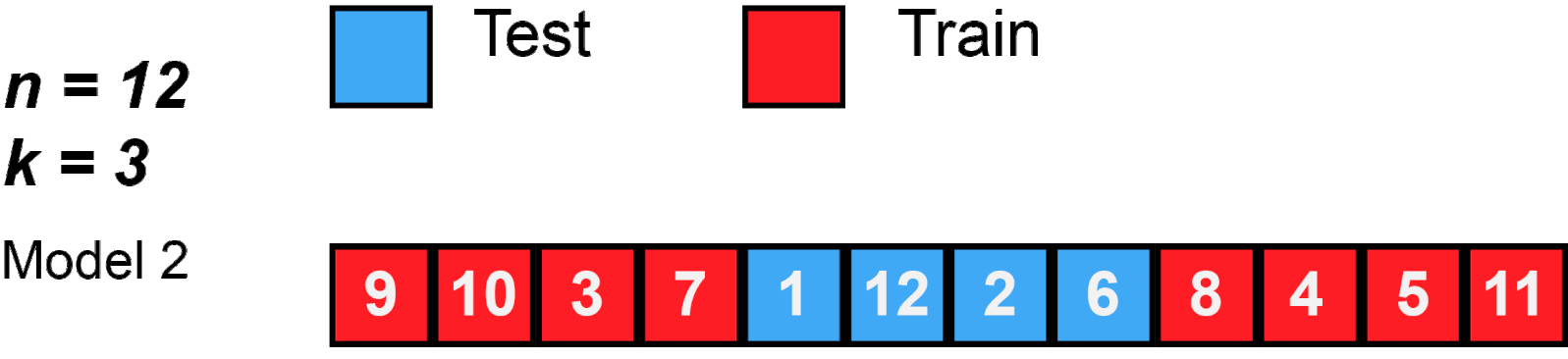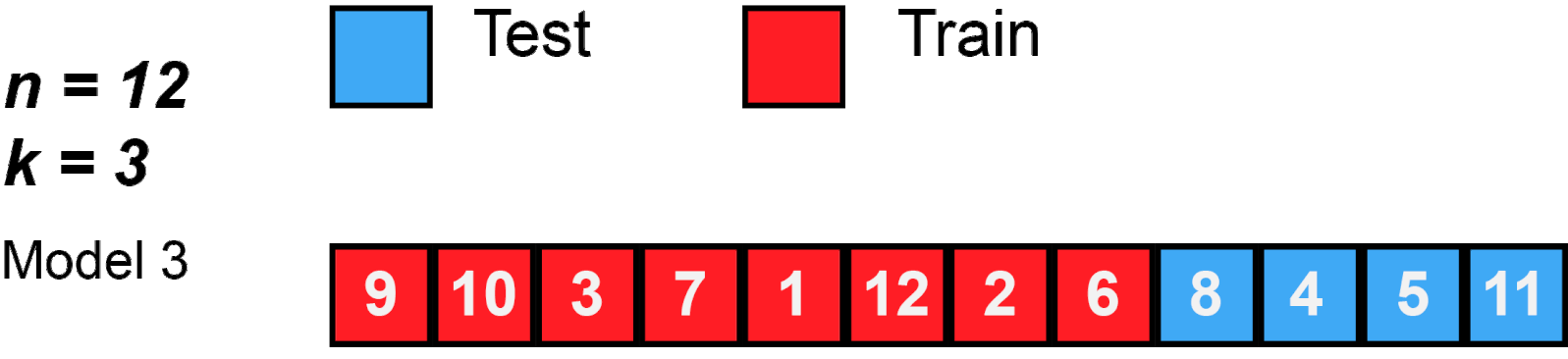Figure 2: K-Fold behavior with n=12 and k=3.
Source: MBanuelos22.

2. Leave One Out

Description: Leave One Out (LOO) is a particular case of K-Fold (k=n). At each iteration, we fit our model on n-1 observations and we predict a value using a single observation at a time, resulting in an almost unbiased estimate for the generalization error. This prediction, however, is not that good since its variance is high given that we used only one point. This process is repeated n times and we compute the LOO estimate for the generalization error by finding the mean of all n MSEs:

.

Figure 3 illustrates an example of LOO with 8 observations.

Pros: As a replacement of the validation set approach, resulting in less bias, given that we train the model in more data. It is a general approach that can be used with all types of predictive models.

To consider: Generally LOO returns high variance for the generalization error estiimator. Also, if n is large, this process can become quite computationally expensive.

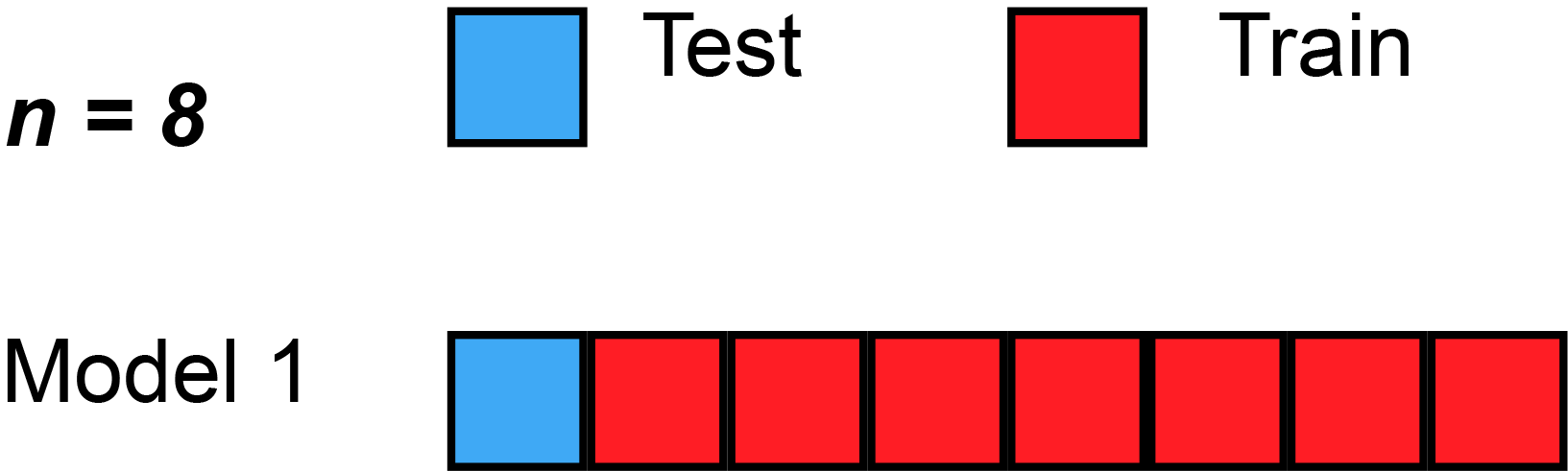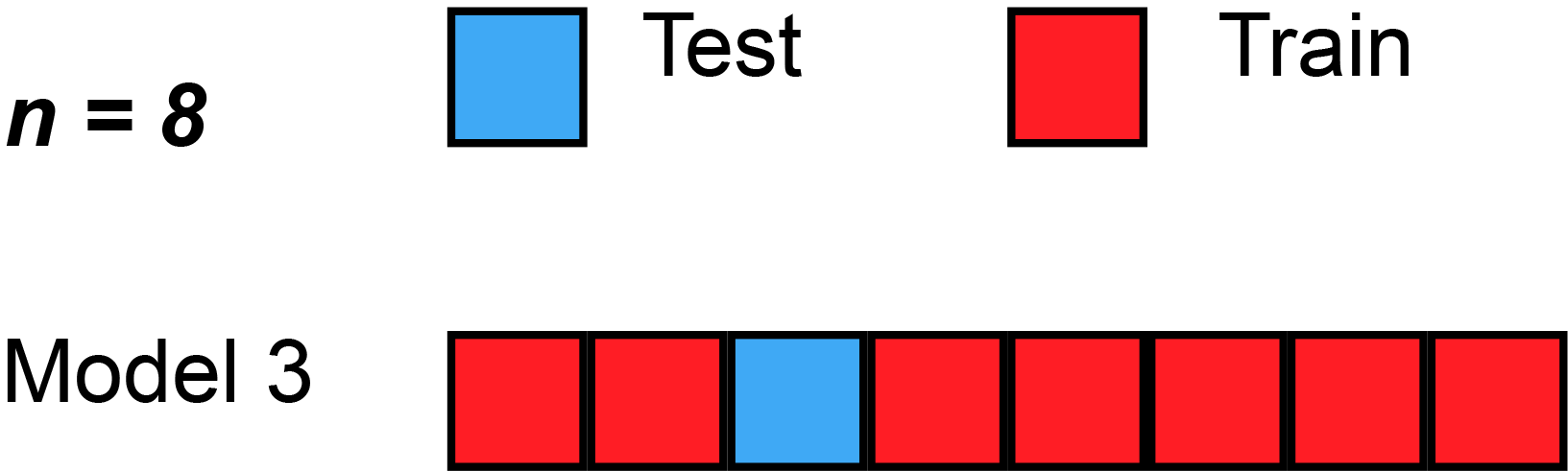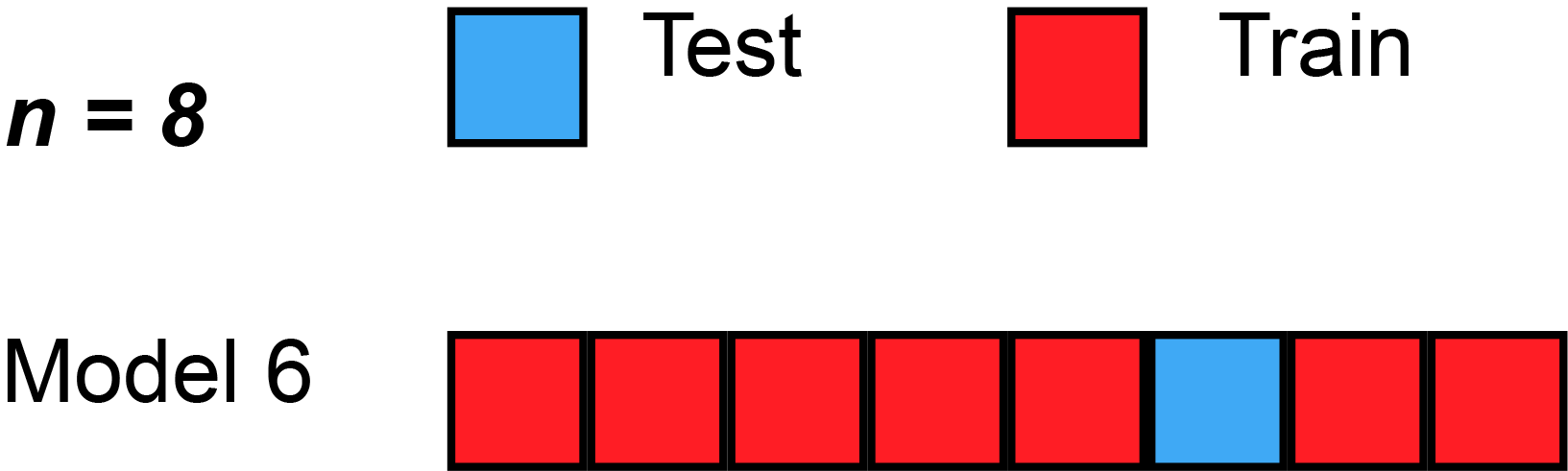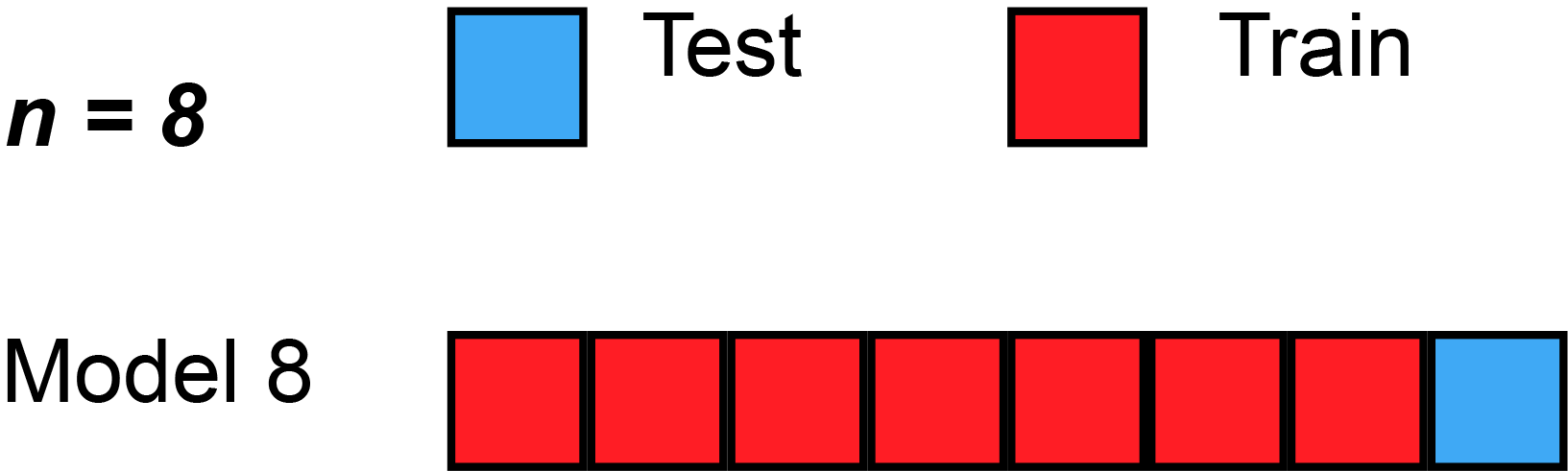Figure 3: LOO behavior with n=8. Source: MBanuelos22.

3. Stratified K-Fold

Description: The Stratified K-Fold method is based on K-Fold as the name suggests, but each fold has pretty much the same proportion of samples of a given class or group. That is, we can split the training making sure that in each fold a particular characteristic is met. If we consider the Titanic dataset, for example, we could split the dataset maintaining the same proportion of the Male and Female in the feature Sex in both the training and test set. This is particularly useful when there is imbalanced data in the target value. We can use the Stratified K-Fold to ensure that we keep the classes proportions, as seen in Figure 4. Notice that class means the dependent variable categories and group can be particular features categories.

When to use it: When it is important to keep groups or classes categories’ proportions in the training and the test sets.

When not to use it: When the feature or target you want to stratify has an unique value.

Figure 4: Stratified K-Fold behavior with k=4. Source: Scikit-learn.

4. Time Series Split

Description: Time Series Split is a method derived from K-Fold. Time series data, however, is not i.i.d. because it is time-dependent. What this approach does, then, is the following: it slipts the data in k folds, but at each iteration i the fold i is the training set and the fold i+1 is the test set. In the next iteration, i+1, all the folds up to i+1 are on the training set and i+2 is the test set, as we can see in Figure 5 for k=4.

When to use it: When we have a dataset based on a time series or data observations from fixed time intervals.

When not to use it: When the data is supposed to be i.i.d. or following a not time-based distribution.

Figure 5: Time Series Split behavior with k=4. Source: Scikit-learn.

Takeaways

Cross-validation is an important technique to obtain more knowledge from the data without the need to acquire more data points. It is a resampling method used to minimize the generalization error before applying a model to the test set. It is not the only approach to estimate the test set, but it is a very popular one. There are many different ways of performing cross-validation and some of them were exposed in this short article, each one with its own assumptions to accomplish the expected result. Although not explicitly discussed here, there is a bias-variance trade-off when deciding on the number of folds to use. The ultimate goal is to achieve a result that does not present neither a high bias nor high variance. Hopefully, now, you understand a little bit better what happens when you do from sklearn.model_selection import ... and know where to find even more information.

References

[1] Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. The elements of statistical learning: data mining, inference, and prediction. Springer Science & Business Media, 2009.

[2] James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. An introduction to statistical learning. Vol. 112. New York: springer, 2013.

[3] Pedregosa et al., Scikit-learn: Machine Learning in Python, JMLR 12, pp. 2825-2830, 2011.